Leetcode 391
Description
我们有 N 个与坐标轴对齐的矩形, 其中 N > 0, 判断它们是否能精确地覆盖一个矩形区域。
每个矩形用左下角的点和右上角的点的坐标来表示。例如, 一个单位正方形可以表示为 [1,1,2,2]。 ( 左下角的点的坐标为 (1, 1) 以及右上角的点的坐标为(2, 2) )。
Sample
Sample 1:
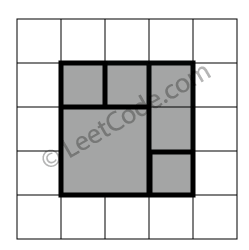
1 2 3 4 5 6 7 8 9 rectangles = [ [1,1,3,3], [3,1,4,2], [3,2,4,4], [1,3,2,4], [2,3,3,4] ] 返回 true。5个矩形一起可以精确地覆盖一个矩形区域。
Sample 2:
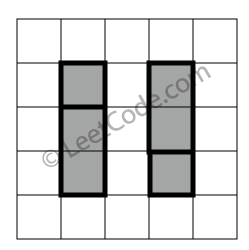
1 2 3 4 5 6 7 8 rectangles = [ [1,1,2,3], [1,3,2,4], [3,1,4,2], [3,2,4,4] ] 返回 false。两个矩形之间有间隔,无法覆盖成一个矩形。
Sample 3:
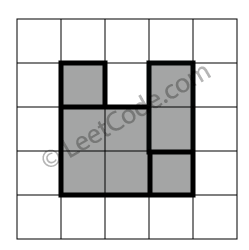
1 2 3 4 5 6 7 8 rectangles = [ [1,1,3,3], [3,1,4,2], [1,3,2,4], [3,2,4,4] ] 返回 false。图形顶端留有间隔,无法覆盖成一个矩形。
Sample 4:
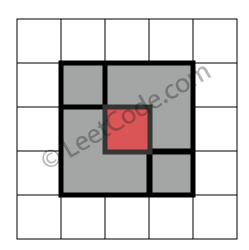
1 2 3 4 5 6 7 8 rectangles = [ [1,1,3,3], [3,1,4,2], [1,3,2,4], [2,2,4,4] ] 返回 false。因为中间有相交区域,虽然形成了矩形,但不是精确覆盖。
Solution
本题非常有意思,第一直觉的反应是搞一个数据结构来维护这个二维平面,比如KD-Tree、二维线段树什么的,来不断查询、插入,复杂度大概是 O(N * log M * log M),其中M表示数据范围。
但是杀鸡焉用牛刀,本题的“完美矩形 ”太特殊了,应该仔细分析完美矩形的性质。
首先,“完美矩形”的框架是很好确定的,直接找左下和右上的点即可。
其次,“完美矩形”一定是面积刚好填充满的,也就是小矩形面积和等于框架面积。
但是,只有面积 的约束太弱了,因为可以很轻易的将完美矩形中的一个小矩形平移,空出来一块,重叠了一块。需要说明的是,在“面积约束”下,反例只能被这么构造:框架内的矩形平移至重叠(允许切割和合并矩形)。
在面积之外,我们还可以关注什么呢?“边”和“点”,显然“点”要简单的多,我们考虑用“点”来约束:
对于“完美矩形”:
框架的四个顶点:只出现一次
内部的点:出现0次、2次、4次
“完美矩形”平移后:内部点的奇偶性一定发生变化,变成出现奇数次。
所以我们根据面积约束和点约束,可以精确的判断是否为“完美矩形”。
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution {public : bool isRectangleCover (vector<vector<int >>& rectangles) int Top = INT_MIN; int Bot = INT_MAX; int Let = INT_MAX; int Rit = INT_MIN; for (auto & rec : rectangles) { Top = max (Top, rec[2 ]); Bot = min (Bot, rec[0 ]); Let = min (Let, rec[1 ]); Rit = max (Rit, rec[3 ]); } int area = (Top - Bot) * (Rit - Let); map<pair<int , int >, int > count; for (auto & rec : rectangles) { area -= (rec[2 ] - rec[0 ]) * (rec[3 ] - rec[1 ]); count[make_pair (rec[0 ], rec[1 ])] ++; count[make_pair (rec[0 ], rec[3 ])] ++; count[make_pair (rec[2 ], rec[1 ])] ++; count[make_pair (rec[2 ], rec[3 ])] ++; } count[make_pair (Bot, Let)] ++; count[make_pair (Bot, Rit)] ++; count[make_pair (Top, Let)] ++; count[make_pair (Top, Rit)] ++; if (area != 0 ) return false ; for (auto par : count) if (par.second & 1 ) return false ; return true ; } };